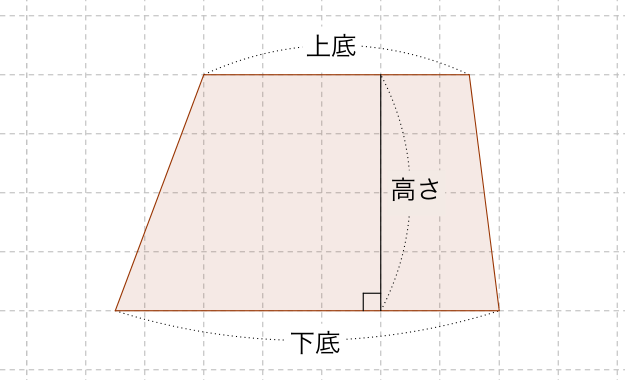
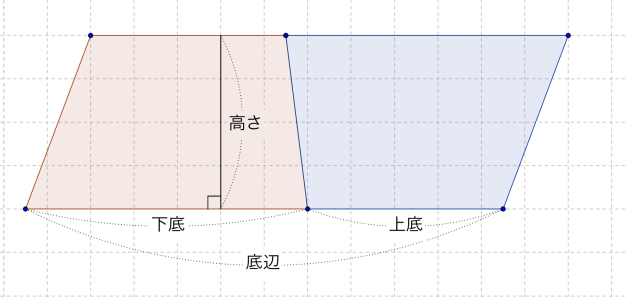
台形の面積の公式
当ページのリンクには広告が含まれています。
台形の面積 \(=\) (上底 + 下底 ) \(\times\) 高さ \(\div\) 2
それでは「台形の面積の公式」を使った「練習問題」を解いてみましょう。「公式の考察」についても合わせてみていきます。
- 練習問題①
上底が 5(cm)、下底が 7(cm)、高さが 4(cm)の台形の面積を求めてください。
- 練習問題②
上底が 2.8(cm)、下底が 3.7(cm)、高さが 4.2(cm)の台形の面積を求めてください。
- 公式の考察
練習問題①
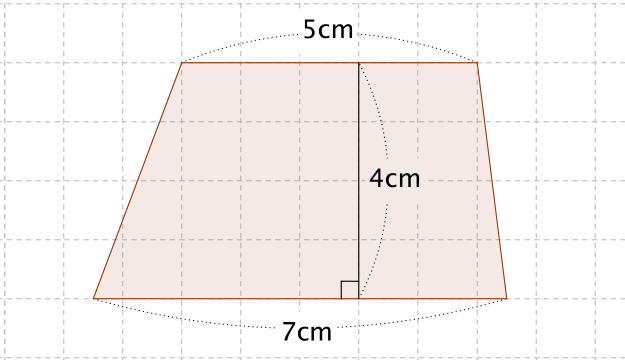
上底が 5(cm)、下底が 7(cm)、高さが 4(cm)の台形の面積を求めてください。
台形の面積を求める公式は
\[ 台形の面積 = (上底 + 下底 ) \times 高さ \div 2 \]なので、
\[ \begin{aligned} 台形の面積 \: &= ( 5 + 7 ) \times 4 \div 2 \\ &= 12 \times 4 \div 2 \\ &= 24 \:(cm^2) \end{aligned} \]になります。
次は小数点を含む台形の面積を計算します。
練習問題②

上底が 2.8(cm)、下底が 3.7(cm)、高さが 4.2(cm)の台形の面積を求めてください。
台形の面積を求める公式は
\[ 台形の面積 = (上底 + 下底) \times 高さ \div 2 \]なので、
\[ \begin{aligned} 台形の面積 \: &= ( 2.8 + 3.7 ) \times 4.2 \div 2 \\ &= 6.5 \times 4.2 \div 2 \\ &= 13.65 \:(cm^2) \end{aligned} \]になります。
公式の考察
なぜ? 台形の面積の公式が「\( ( 上底 + 下底 ) \times 高さ \div 2 \)」になるのかを考えてみましょう。
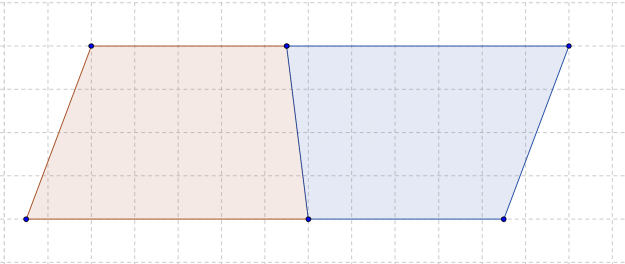
「青色の台形」をひっくり返して、「赤色の台形」とくっつけると……
平行四辺形になりますね。
\[ 平行四辺形の面積 = 底辺 \times 高さ \]なので、「赤色の台形」と「青色の台形」をくっつけた平行四辺形の面積は
\[ \begin{aligned} 平行四辺形の面積 \: &= 「赤色の台形」の面積 + 「青色の台形」の面積 \\ \: &= 底辺 \times 高さ \\ \: &= ( 上底 + 下底 ) \times 高さ \end{aligned} \]になります。
台形(赤色) と 台形(青色)は同じ形なので、
\[ 台形(赤色)の面積 = 台形(青色)の面積 \]ですね。
よって、(赤色の)台形の面積は
\[ 台形の面積 = (上底 + 下底 ) \times 高さ \div 2 \]となります。