円の面積の公式
当ページのリンクには広告が含まれています。
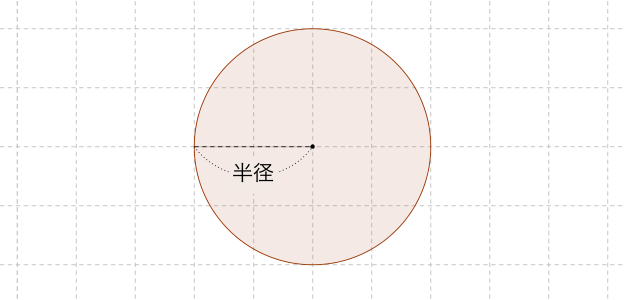
円の面積 \(=\) 半径 \(\times\) 半径 \(\times\) 円周率
それでは「円の面積の公式」を使った「練習問題」を解いてみましょう。
- 練習問題①
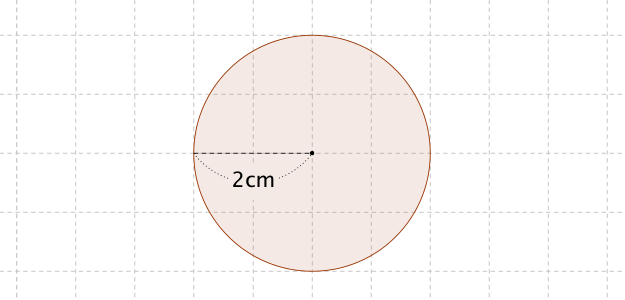
半径が 2(cm)の円の面積を求めてください。ただし円周率を 3.14とします。
- 練習問題②
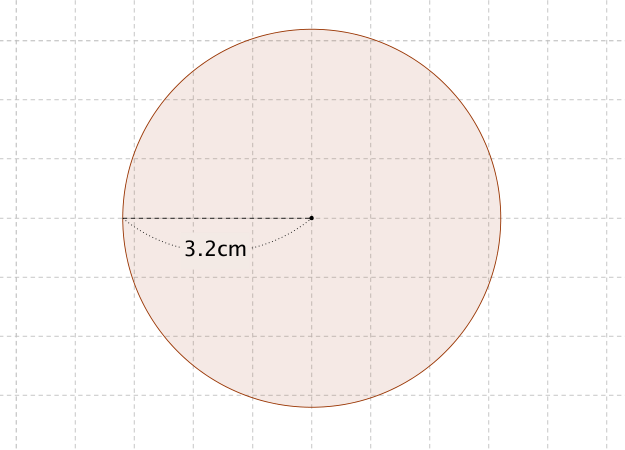
半径が 3.2(cm)の円の面積を求めてください。ただし円周率を 3.14とします。
- 練習問題③
面積が 113.04(cm2)の円の半径を求めてください。ただし円周率を 3.14とします。
練習問題①
半径が 2(cm)の円の面積を求めてください。ただし円周率を 3.14とします。
円の面積を求める公式は
円の面積 \(=\) 半径 \(\times\) 半径 \(\times\) 円周率
なので、円の面積を \(S\) とすると
\[ \begin{aligned} S \: &= 2 \times 2 \times 3.14 \\ &= 12.56 \:(cm^2) \end{aligned} \]になります。
練習問題②
半径が 3.2(cm)の円の面積を求めてください。ただし円周率を 3.14とします。
円の面積を求める公式は
円の面積 \(=\) 半径 \(\times\) 半径 \(\times\) 円周率
なので、円の面積を \(S\) とすると
\[ \begin{aligned} S \: &= 3.2 \times 3.2 \times 3.14 \\ &= 32.1536 \:(cm^2) \end{aligned} \]になります。
練習問題③
面積が 113.04(cm2)の円の半径を求めてください。ただし円周率を 3.14とします。
円の面積を求める公式は
円の面積 \(=\) 半径 \(\times\) 半径 \(\times\) 円周率
なので、半径を \(x\) とすると
\[ \begin{aligned} 113.04 \: &= x \times x \times 3.14 \\ x \times x \: &= 113.04 \div 3.14 \\ x \times x \: &= 36 \\ x \: &= 6 \:(cm) \end{aligned} \]になります。